荷物を押す回数
荷物を押すとは
この分析のページ全体を通して荷物を押す回数とは、荷物が動いたマス目の数です。同じ荷物を連続で押した場合でも1マスごとにカウントします。言葉を縮めて「荷押し回数」と書くこともあります。
まえがきに書いた意外な性質の1つは、解答の荷押し回数は偶数奇数が決まっているという規則です。
1つの問題面に対して荷押し回数が異なる様々な解き方を試しても、荷押しの偶数奇数はどちらか一方しか現れません。その理由を以下で説明します。
偶数奇数の基礎
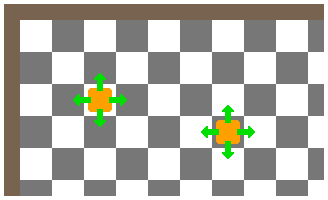荷押しの偶数奇数は、右図のようなチェス盤状の白黒の床に荷物を置いた状況で考察します。
チェス盤は上下左右の色が反転しているので、荷物が1マス移動する度に白は黒、黒は白に変わります。
荷物が1個なら、荷押しが奇数のときに色が反転し、荷押しが偶数のときに開始の色に戻ります。
この性質により、開始時の色と格納点の色が等しい問題は解答が偶数になり、色が異なる問題は解答が奇数になることが決まっています。
基礎から全体に
荷物が2個の問題は、格納する場所を交換したケースについて、それぞれ偶数奇数を調べる必要がありそうですが、実際は、荷物の初期配置を考察することで条件が整理できます。
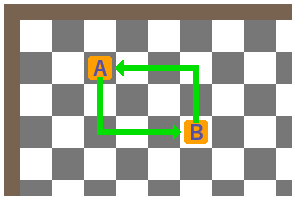右図のように、初期配置の荷物2個をＡ,Ｂとすると、ＡをＢの位置に移動して、ＢをＡの位置に移動すると、基礎の性質により、荷押し回数は必ず偶数になります。
このことから、ＡとＢの格納場所を交換してもトータルの偶数奇数には影響がないと判断できます。
この条件の整理により、荷物1個と同様に、荷物2個の解答も偶数奇数が決まっていることが分かります。
また、荷物が3個以上の問題も、荷物2個の交換を繰り返すことで荷物の区別がなくなるので、倉庫番の問題は例外なく、解答の偶数奇数が一方に決まっていると結論付けることができます。
以上が解答の偶数奇数の説明ですが、私がこの規則性に気がついたのは、解答の値を調べて見つけたのではなく、ある疑問を解消しようとした結果からヒントを得ました。
その疑問と考察から見えてきた倉庫番の構造的な仕組みを次項で説明します。
奇数はないのか
あるとき、任意の荷物配置からスタートして、再びその配置に戻る行程について考えていました。
最も簡素な荷物1個で考えると、荷押しが2回、4回、6回のときに元の位置に戻りますが、1回、3回、5回で戻る順路は見つかりません。
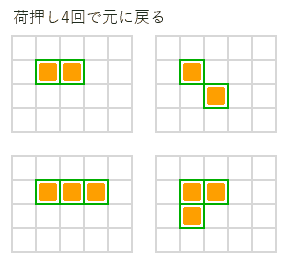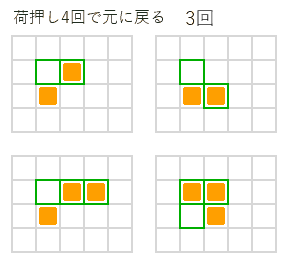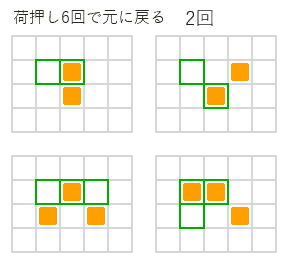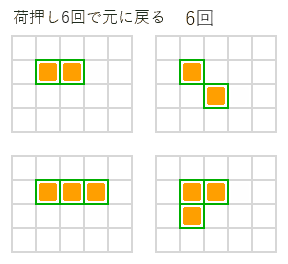右図のように荷物が2個や3個の場合でも、荷押し4回、6回で元の配置に戻る方法は簡単に見つかりますが、3回、5回、7回の方法はなさそうに思えます。
しかし、実際に偶数でしか元に戻らないとしても、偶数で戻る例を挙げるだけでは証明にならないので、奇数で戻るケースがないと言い切ることができずにいました。
そこで、もし本当に偶数回でしか元に戻らないなら、どうにか画一的に説明できないかと考えた末に行き着いたのが、荷物をチェス盤に乗せてみるという方法でした。
市松から分かること
右の図は、白に4個、黒に3個の荷物が置かれたチェス盤状の倉庫です。これを初期状態とします。
これに荷押しを1回加えると、白か黒の一方が1個減って他方が1個増え、白3黒4あるいは白5黒2、のどちらかになります。
このときの荷物の偶数奇数に着目すると、白も黒も初期状態の反対になっています。
続けてもう1押し加えると、偶数奇数が再び反転して初期状態と一致するようになり、それ以降も荷押しを加える度に、反転、一致を交互に繰り返します。
白黒それぞれの荷物の状態をまとめると、全ての局面は次の2つのグループに分かれます。
つまり、倉庫番の局面は、荷物を1マス押すごとに上記のグループを行き来しています。
当然ですが、(1)の局面と(2)の局面が一致することはないので、これが最初に浮かんだ『同一局面に戻るのは荷押しが偶数のときだけか？』という疑問の証明になります。
また、全ての荷物が格納された局面も両方のグループに含まれることはないので、これが手掛かりになって、解答の偶数奇数が一方に決まっている規則に気がつくことになりました。
その後いろいろな問題で試して、その通りになっていることを確認しています。